Improving ECG Analysis with Stationary Wavelet Transform (SWT) Denoising

Introduction

Electrocardiography (ECG or EKG) is a vital tool in cardiology and healthcare for monitoring and diagnosing heart-related conditions. An ECG records the electrical activity of the heart over time, typically represented as a waveform. Analyzing ECG signals allows healthcare professionals to detect abnormalities, assess heart health, and make informed clinical decisions. However, ECG signals are often prone to noise and interference, making accurate analysis challenging, hence, noise reduction plays a critical role in enhancing the quality and interpretability of data.

Such noise can be overcome by signal processing techniques and Stationary Wavelet Transform (SWT) is one such powerful tool utilized in this endeavor, which provides a multi-resolution analysis of a signal. This technique is particularly effective in denoising applications, as it allows for the isolation and removal of unwanted noise while preserving the essential features of the signal. In this article, we will delve into the principles of SWT for denoising and provide a practical Python project with code snippets that demonstrate its application.

In this article, we will explore how the Stationary Wavelet Transform (SWT) can be employed to enhance the quality of ECG data by denoising, and we will provide a Python project with code snippets. Additionally, we will introduce relevant ECG analysis metrics and showcase improvements through Power Spectral Density (PSD) and Signal-to-Noise Ratio (SNR) comparisons.

Understanding ECG Analysis

ECG analysis involves the examination of ECG signals to extract valuable information about cardiac activity. Key metrics and analyses include:

• R-Peak Detection: The detection of R-peaks, which represent the electrical depolarization of the ventricles, is essential for determining heart rate and assessing rhythm irregularities.
• Heart Rate: The heart rate, typically measured in beats per minute (BPM), indicates how fast the heart is beating and is essential for assessing cardiac function.
• Heart Rhythm: Analyzing the intervals between R-peaks helps identify rhythm abnormalities, such as arrhythmias, which can have serious clinical implications.
• ST-Segment Analysis: Changes in the ST-segment can reveal myocardial ischemia or injury, making it a critical metric for diagnosing heart conditions.
• T-Wave Analysis: Abnormalities in T-wave morphology can indicate various cardiac pathologies, including electrolyte imbalances and myocardial ischemia.
• P-R Interval: The P-R interval represents the time it takes for the electrical impulse to travel from the atria to the ventricles and is critical for assessing atrioventricular conduction.
• Signal Quality: Ensuring the quality of the ECG signal is crucial for accurate analysis. Noise and artifacts can distort the waveform and affect diagnostic accuracy.

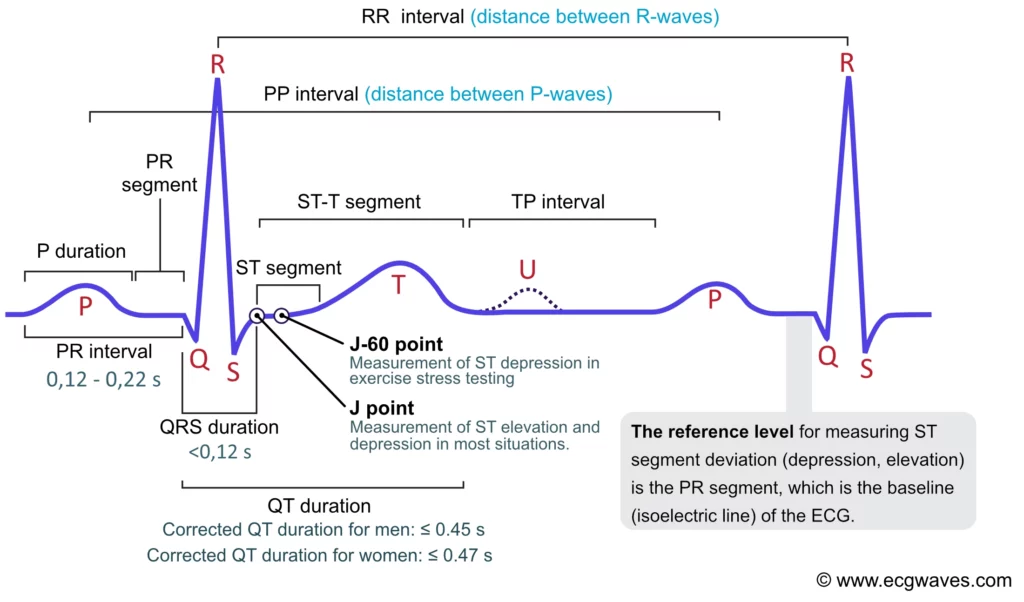
The above picture sourced from a descriptive article, identifies the several metrics mentioned above which can be extracted from an ECG readings. The article further delves into what each of those metrics practically imply and how they can be utilized in order to determine cardioascular issues by trained doctors/ analysts.

Denoising ECG Signals with SWT

The Stationary Wavelet Transform (SWT) is an extension of the Discrete Wavelet Transform (DWT), uniquely suited to the denoising of signals with varying lengths, like ECG signals. It decomposes an ECG signal into multiple scales using wavelets, which are mathematical functions that describe signal features at different resolutions. The key steps in applying SWT for ECG signal denoising are as follows:

• Decomposition: The ECG signal is decomposed into different scales using wavelets. Each scale captures specific frequency components, allowing the separation of the ECG signal from noise.
• Thresholding: Coefficients obtained from the decomposition are subject to thresholding. Noise or insignificant signal details are either reduced or set to zero to minimize their impact.
• Reconstruction: The denoised ECG signal is reconstructed from the thresholded coefficients, retaining vital ECG features while reducing noise.

Python Implementation

To demonstrate how SWT can be applied to denoise ECG signals, we will use Python with the PyWavelets library. First, ensure you have PyWavelets installed:

pip install PyWavelets

Now, let’s create a Python script to perform ECG denoising using SWT and generate PSD and SNR comparisons:

import numpy as np
import pandas as pd
import pywt
import matplotlib.pyplot as plt
import scipy.signal as spsig

# Functions available in ECGAnalyses
import ECGAnalyses as eca
# rr_intervals          = np.diff(r_peaks) / sampling_rate
# heart_rate            = calculate_heart_rate(r_peaks)
# rhythm_status         = analyze_rhythm(rr_intervals)
# st_segment_changes    = analyze_st_segment(denoised_ecg, r_peaks)
# t_wave_status         = analyze_t_wave(denoised_ecg)
# pq_interval_status    = analyze_pq_interval(rr_intervals)


# Read ECG dataset (change filename here) [assuming CSV format]
dataTable = pd.read_csv('filename.csv')
[sets, nSamples] = dataTable.shape
print('Signal sets in table, ' + str(dataTable.shape))

fs = 125
timeAxis = np.linspace(1, nSamples / fs, nSamples)

# Iterate over each signal
for j in range(0, sets - 1):
    
    # Option to enable user input for: wavelet families, order, level, noise Threshold
    # waveletChoose = input('Choose a wavelet family for conducting the spectral De-noising')
    # orderChoose = input('Choose the order for spectral De-noising')
    # levelChoose = input('Choose the level for spectral De-noising')
    # setThreshold = input('Enter threshold for De-noising detail coefficients')

    # Set wavelet transform parameters
    waveletChoose = 'db'
    orderChoose = 4
    levelChoose = 8
    setThreshold = 0
    waveletOrder = waveletChoose + str(orderChoose)
    
    # Load signal data
    signal = dataTable.iloc[j, :]

    # Do the DWT transform
    if levelChoose == 1:
        cApproximate, cDetailed = pywt.dwt(signal, waveletOrder)
    else:
        wv = pywt.Wavelet(waveletOrder)
        multilevelCoefficients = pywt.wavedec(signal, waveletOrder, level=levelChoose)

    # Declare wavelet to the library
    wv = pywt.Wavelet(waveletOrder)

    # Use thresholding to isolate approx. coefficients & reconstruct
    if levelChoose == 1:
        # Set the detailed coefficients above the desired noise threshold to the desired value
        for k in range(0, len(cDetailed) - 1):
            if abs(cDetailed[k]) >= setThreshold:
                cDetailed[k] = 0

        # Reconstruct using the noise thresholded coefficients
        denoised_ecg = pywt.idwt(cApproximate, cDetailed, waveletOrder, mode='constant')

    else:
        # Set the detailed coefficients at the nth level of the transform that are above the threshold to the desired value (0 here)
        cDetailed = multilevelCoefficients[1]
        for k in range(0, len(cDetailed) - 1):
            if abs(cDetailed[k]) >= setThreshold:
                cDetailed[k] = 0
        multilevelCoefficients[1] = cDetailed

        # Reconstruct using the noise thresholded coefficients
        denoised_ecg = pywt.waverec(multilevelCoefficients, wv)

OR, you can also utilize the direct swt and threshold functions in the PyWavelet library to decompose and threshold the ECG signal using SWT and threhsold methods respectively.

    coeffs = pywt.swt(signal, waveletORder, level=levelChoose)

    # Apply thresholding through(e.g., soft thresholding)
    threshold = 0.1 * np.std(coeffs[-1][-1])  # Adjust the threshold value as needed
    thresholded_coeffs = [pywt.threshold(c, threshold, mode='soft') for c in coeffs]

    # Reconstruct the denoised ECG signal
    denoised_ecg = pywt.iswt(thresholded_coeffs, wavelet)

We have obtained a cleaner signal which has been de-noised using the Stationary Wavelet Transform. Now, we utilize the denoised signal to extract cardiac health metrics using standard statistical metrics utilized in literature.

The logic for ST-segments and T-Wave are general implementations to showcase functionality, more advanced and application specific algorithms can be sought out in the literature. Please feel free to seek a pull request if you possess updated knowledge on obtaining these standardized metrics from the GIT repo.

    # Find R-peaks in the ECG signal
    peaks, _ = eca.find_r_peaks(denoised_ecg, height=0.2, fs)  # Adjust threshold as needed

    # Calculate the heart rate for the given signal data from R-peaks
    HR = eca.calculate_heart_rate(r_peak_indices, sampling_rate=1000)

    # Analyze hear rhythm based on R-R intervals
    HeartRhythmState = eca.analyze_rhythm(rr_intervals, threshold=0.15)

    # Calculate ST-segments and anlayze changes
    STsegmentState = eca.analyze_st_segment(ecg_signal, r_peak_indices, sampling_rate=1000)

    # Analyze T-waves for abnormalities
    TwaveState = eca.analyze_t_wave(ecg_signal, threshold=0.1)

    # Use P-peaks and QRS intervals to extract the the P-R intervals
    PTintervalState = eca.analyze_pr_interval(rr_intervals, sampling_rate, threshold=0.2)

Calculating the Power Spectral Density and SNR

    # Find PSD > SNR etc.
    (f_L, Sig) = spsig.welch(signal, fs)
    # Remove the few beginning and ending samples to remove transitional noise
    (f_L, Noise) = spsig.welch(denoised_ecg[5: len(denoised_ecg) - 5], fs)  
    
    # absSignalPower = np.abs(sum(Sig))**2
    # absNoisePower = np.abs(sum(Noise))**2
    signalPower = sum(Sig)
    noisePower = sum(Noise)
    print('Signal power' + str(round(signalPower, 4)) + ', Noise: ' + str(round(noisePower, 4)))

    snrCal = 20 * math.log(signalPower / noisePower, 2)
    snrAtPeaks = 10 * np.log10(np.sum(signal[peaks] ** 2) / np.sum((signal - denoised_ecg) ** 2))
    
    # You can also use the direct function for PSD provided in the matplotlib library

    # Matplotloib: Power Spectral Density (PSD)
    frequencies, psd_original = plt.psd(signal, NFFT=1000, Fs=1000, noverlap=0)
    _, psd_denoised = plt.psd(denoised_ecg, NFFT=1000, Fs=1000, noverlap=0)

    # Display the results
    plt.figure(figsize=(10, 6))
    plt.subplot(2, 1, 1)
    plt.title("Original ECG Signal vs. Denoised ECG Signal")
    plt.plot(signal, label="Original ECG Signal")
    plt.plot(denoised_ecg, label="Denoised ECG Signal")
    plt.legend()

    plt.subplot(2, 2, 3)
    plt.title("PSD Comparison")
    plt.semilogy(frequencies, psd_original, label="Original ECG PSD")
    plt.semilogy(frequencies, psd_denoised, label="Denoised ECG PSD")
    plt.legend()

    plt.subplot(2, 2, 4)
    plt.title("Signal-to-Noise Ratio (SNR)")
    plt.text(20, 20, f"SNR: {snr:.2f} dB")

    plt.tight_layout()
    plt.show()

# Next iteration runs for the next signal  

Conclusion

The Stationary Wavelet Transform (SWT) is a valuable tool for improving the analysis of ECG signals by reducing noise while preserving essential diagnostic information. In this article, we introduced ECG analysis metrics, discussed the benefits of ECG denoising using SWT, and provided a Python project with code snippets. The inclusion of Power Spectral Density (PSD) and Signal-to-Noise Ratio (SNR) comparisons highlights the effectiveness of this methodology. Accurate ECG analysis is vital for early diagnosis and appropriate medical intervention, making denoising techniques like SWT invaluable in clinical settings.

Takeaways

• What is Stationary Wavelet Transform and how is it different from Discrete Wavelet Transform.
• Cardio-vascular health indicators that are identifiable from Electro-Cardiogram data.